数据结构(2)-栈和队列

引言

栈与队列是两种重要的线性结构，本节除了采用前一节提到的顺序线性表和链式线性表来分别实现 这两种特色的线性表。还根据书上内容实现了一些具体应用

栈

栈可以想像成在一个桶子里堆积木，先放的被压在了下面，不能从中间抽，每次只能从最上面拿。所以栈的特点就是后进先出。先放进来的被压倒最下面，最后放的在最上面所以最先能拿出来。

顺序线性表实现栈

可以采用顺序线性表来实现栈，除了用一个指针指向连续空间的首地址，还需要用一个指针指向最后放入的数据。因为栈是后进先出，因此最先放入数据的首空间地址指针就是底(base), 而最后放入数据的空间位置则是出口(Top).
为了方便栈判空，我们可以定义top==base时栈为空，则插入一个数据后Top就要往后移动一位。因此栈中数量可以用Top-base求得。这样top就不是指向最后一个元素，而是指向最后一个数据的后一个空间。也就是下一个要放入数据的空间。
栈的结构体定义以及常用的初始化，入栈，出栈，打印栈空间代码如下：

#include<stdio.h>
#include<stdlib.h>
#define Stack_init_size 100
#define stack_increment 10
typedef int SElemType;
typedef struct Stack{
	SElemType *base;
	SElemType *top;
	int stacksize;
}SqStack;
void initStack(SqStack &S){// 初始化栈
	S.base = (SElemType*)malloc(Stack_init_size*sizeof(SElemType));
	S.top = S.base;
	S.stacksize = Stack_init_size;

}
bool PopStack(SqStack &S, SElemType &e){//  获取栈顶数据，并删除原数据，即出栈
	if(S.top == S.base) return false;
	S.top-=1;
	e = *S.top;
	//其实等价于e = *--S.top;
	return true;

}
bool GetStack(SqStack &S, SElemType &e){ // 获取栈顶数据 不删除原数据
	if(S.top==S.base) return false;
	e = *(S.top-1);
	return true;

}
void Push(SqStack &S, SElemType &e){ //将数据e插入栈
	if(S.top-S.base>=S.stacksize){ //原空间放满了
		S.base = (SElemType*)realloc(S.base,(S.stacksize+stack_increment)*sizeof(SElemType)); // 追加空间 
		S.top = S.base+S.stacksize;
		S.stacksize += stack_increment;
	}
	*S.top = e; //数据插入栈头
	S.top+=1; //栈头指针往后移动
}
void CreatStack(SqStack &S, int n){ //给栈输入n个数
	int e;
	while(n--){
		scanf("%d",&e); //每输入一个数
		Push(S,e);  //插入到栈头
	}
}
void print_Stack(SqStack &S){ //打印栈（这种方式只是用来看栈里面数据顺序是否正确，真正的栈操作应该从top开始向base）
	printf("base");
	SElemType *p = S.base; //用一个指针去遍历栈从栈底开始
	while(p!=S.top){ //一直遍历到栈头
		printf("->%d",*p);
		p=p+1;
	}
	printf("->Top\n");
}
int main(){
	SqStack s;
	SElemType e;
	initStack(s);
	CreatStack(s,10);
	print_Stack(s);
	PopStack(s,e);
	printf("%d",e);
	return 0;
}

线性链表实现栈

其实逆序创建一个链表就是在创建一个栈（先输入的数据在后面，后输入的在前面），这样创建的链表要出栈也很容易，直接把头结点后面的第一个数据结点输出即可。
具体代码如下

#include<stdio.h>
#include<stdlib.h>
#define Stack_init_size 100
#define stack_increment 10
typedef int SElemType;
typedef struct SNode{
	SElemType data;
	struct SNode* next;
}SNode, *LinkStack;
void init_Stack(LinkStack &l){ //初始化一个空栈
	l = (LinkStack)malloc(sizeof(SNode));
	l->data = 0;
	l->next = NULL;
}
void Creat_LinkStack(LinkStack &l, int n){ //创建一个长度n 的链表栈(即链表的逆序创建)
	LinkStack p;
	while(n--){ //逆序创建
		p = (LinkStack) malloc(sizeof(SNode)); //创界数据结点分配空间
		scanf("%d", &p->data);// 输入数据
		p->next = l->next;
		l->next = p;
		/* 另一种调用子函数的写法
		int a;
		scanf("%d", &a);
		Push(l,a);
		*/
	}
}
void Push(LinkStack &l, SElemType e){//入栈数据e
	LinkStack p = (LinkStack)malloc(sizeof(SNode));
	p->data = e;
	//逆序创建的原理入栈
	p->next = l->next;
	l->next = p;

	l->data+=1; //栈长度+1
}
bool Pop(LinkStack &l, SElemType &e){
	if(l->data<1) return false; //空栈
	LinkStack p = l->next; // p 指向第一个数据结点(栈头结点)。
	e = p->data;
	l->next = p->next;//把这个结点从栈中拿出来
	l->data -= 1;
	free(p);//释放空间
	return true;
}
void print_Stack(LinkStack &l){
	LinkStack p = l->next; //p指向第一个数据结点
	while(p!=NULL){
		printf("%d ",p->data);
		p = p->next;
	}

}
int main(){
	LinkStack l;
	SElemType e = 7;
	init_Stack(l) //初始化栈
	Creat_LinkStack(l,5); //创建 一个长度5的栈
	print_Stack(l); // 打印栈
	Push(l,e); // 数据e入站
	print_Stack(l); // 打印栈
	Pop(l,e);  // 出栈 栈顶元素放在e
	printf("%d",e);
	print_Stack(l);print_Stack(l);
	return 0;
}

栈的应用

数制转换

顾名思义，用栈来实现十进制到其他进制的转换。十进制数N到其他任意进制d的转换原理是N = (N div d) x d + N mod d (其中:div为整除运算，mod为取余运算)。
例子如下：

所以，直接把输入的数取余8然后放入栈，然后这个数=其取整8 直到这个数=0，再按栈中顺序输出就是其八进制了。
代码如下，具体子函数实现和上面一样

int main(){
	LinkStack l;
	init_Stack(l);
	int number = 1348; //十进制 1348
	while(number){ //不为0时 
		Push(l, number%8);  //余数入栈
		number /= 8; // 除8取整
	}
	//出栈 输出
	while(Pop(l,number)){//栈不为空时持续出栈
		printf("%d ",number);
	}
	return 0;
}

括号匹配

即检查一串字符中各种不同括号的左右括号数量是否匹配比如 [{]} 和{[}就不匹配，而{[{([][])}]} 则是正确的。所以其原理是建立一个栈 遇到左括号无论哪种都入栈。
若遇到右括号则出栈，并看出栈的左括号和它是否类型匹配。
源码如下:

typedef char SElemType; //这里就体现了类型定义的优势，上面代码就不用把大量int改成char了。当然输入输出需要改下类型匹配，如果用的C++的cin cout就输入输出都不用改
int main(){
	LinkStack l;
	init_Stack(l);
	int flag = 0; //0 表示字符串括弧合法，1表示不合法
	SElemType e,e_l;
	while(scanf("%c",&e),e!='\n'){ //输入换行结束
		if(e==']'){
			if(!Pop(l,e_l)||e_l!='['){//栈为空 或者出栈括弧不匹配则直接退出
				flag = 1;
				break;
			}
		}else if(e==')'){
			if(!Pop(l,e_l)||e_l!='('){//栈为空 或者出栈括弧不匹配则直接退出
				flag = 1;
				break;
			}
		}else if(e== '}'){
			if(!Pop(l,e_l)||e_l!='{'){//栈为空 或者出栈括弧不匹配则直接退出
				flag = 1;
				break;
			}
		}else{ //不是以上三种则是左括弧 则入栈
			Push(l,e);
		}
	}
	if(flag==0&&l->data==0){//做完上述操作未发现错误，且栈为空
		printf("success");
	}else{
		printf("error");
	}
	return 0;
}

行编辑程序

一个简单的行编辑程序的功能是：接受用户从终端输入的程序或数据，并存入用户的数据区。由于用户在终端上进行输人时，不能保证不出差错,因此,若在编辑程序中，“每接受一个字符即存入用户数据区”的做法显然不是最恰当的。
较好的做法是，设立一个输入缓冲区,用以接受用户输入的一行宇符,然后逐行存入用户数据区。允许用户输人出差错,并在发现有误时可以及时更正。例如，当用户发现刚刚键入的一个字符是错的时,可补进一个退格符“＃”，以表示前一个字符无效;
如果发现当前键入的行内差错较多或难以补救,则可以键入一个退行符“@”，以表示当前行中的字符均无效。例如，假设从终端接受了这样两行字符：
whli##ilr#e(a#s)
outcha@putchar(s=#++);
则实际有效的是下列两行：
while(s)
putchar(s++);

void Empty(LinkStack &l){ //栈放空
	LinkStack p = l->next;
	if(p!=NULL){
		l->next = p->next;
		free(p);
		p = l->next;
	}
	l->data = 0;
}
void print_empty(LinkStack &l){ //顺序打印栈并清空
	//打印有效字符。考虑到栈后进先出，如果按栈顺序打印则是倒的，因此我们先把这个栈出栈插入另外 一个栈 ，给他调个头。
	char e;
	LinkStack p;
	init_Stack(p);
	while(l->data>0){
		Pop(l,e);
		Push(p,e);
	}

	//然后出栈p打印
	while(p->data>0){
		Pop(p,e);
		printf("%c",e);
	}
	printf("\n");
}
int main(){
	LinkStack l;
	init_Stack(l);
	int flag = 0; //0 表示字符串括弧合法，1表示不合法
	SElemType e,e_l;
	scanf("%c",&e); 
	while(e!=EOF){
		while(e!=EOF&&e!='\n'){
			switch(e){
				case '#': Pop(l,e); break; //输入#退栈
				case '@': Empty(l); break; //输入@清空栈
				default: Push(l,e); break; //其他字符入栈
			}
			scanf("%c",&e);//接收下一个
		}
		print_empty(l);
		if(e!=EOF){
			scanf("%c",&e);//接收下一个
		}
		//换行符 打印，然后清空栈
	}
	print_empty(l);
	return 0;
}

迷宫求解

求迷宮中从入口到出口的所有路径是一个经典的程序设计问题。由于计算机解迷宫时，通常用的是“穷举求解”的方法，即从入口出发，顺某 一方向向前探索，若能走通，则继续往前走;
否则沿原路退回,换一个方向再继续探索，直至所有可能的通路都探索到为止。为了保证在任何位置上都能沿原路退回，显然需要用一个后进先出的结构来保存从入口到当前位置的路径。
因此,在求迷宫通路的算法中应用“栈”也就是自然而然的事了。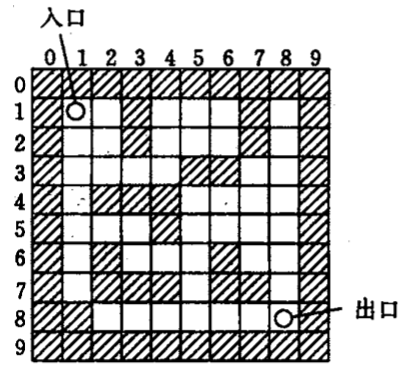

算是本书比较复杂的几个算法之一，其实栈的应用不多，只是用来记录走过的路径，方便回退。主要是如何找方向，如何循环走下去，如何判断下一步可不可以走(是墙或者是走过的路)
解题思路: 迭代+栈。栈采用链式结构，结点中包含三个数据，当前结点所表示位置的(x,y)以及在当前位置要走的下一步方向，我们可以用0表示向上，1表示向左，2表示向下，3表示向右。然后0，1，2，3 循环向四个方向找是否可以走，可以则记录当前位置和下一步要走的方向。比如在(1,3)位置发现向上，向左都不能走，向下时可以走了则入栈(1,3,3)表示这个方向走不通时，回退到（1，3）后就直接向右走就行。
然后为了防止走 走过的路，可以把走过的路在地图上标记。实现时直接用bool型二维数组生成地图，可以走的地方是true，不能走的地方是false, 那么在找路径的过程中把走过的地方也改成false 即可。
实现代码如下:

#include<stdio.h>
#include<stdlib.h>
typedef struct Node{
	int x;
	int y;
	int ind; //0上 1左 2下 3右
	struct Node *next;
}Node, *List;
// 创建一个地图 false为不可以走，true为可以走
bool map[10][10]={
{false,false,false,false,false,false,false,false,false,false},
{false,true,true,false,true,true,true,false,true,false},
{false,true,true,false,true,true,true,false,true,false},
{false,true,true,true,true,false,false,true,true,false},
{false,true,false,false,false,true,true,true,true,false},
{false,true,true,true,false,true,true,true,true,false},
{false,true,false,true,true,true,false,true,true,false},
{false,true,false,false,false,true,false,false,true,false},
{false,false,true,true,true,true,true,true,true,false},
{false,false,false,false,false,false,false,false,false,false}}; 
// 输出找到的路径
void print_L(List &l){
	List p = l->next;
	while(p!=NULL){
		printf("(%d, %d)",p->x,p->y);
		p = p->next;
	}
	printf("\n");
}
//初始化一个链表栈
void init(List &l){
	l = (List)malloc(sizeof(Node));
	l->x = 0;
	l->y = 0;
	l->ind = 0;
	l->next = NULL;
}
//入栈
void Push(List &l,int x,int y,int ind){
	List p = (List)malloc(sizeof(Node));
	p->x = x;
	p->y = y;
	p->ind = ind;
	p->next = l->next;
	l->next = p;
}
//出栈
bool Pop(List &l,int &x, int &y, int &ind){
	if(l->next == NULL) return false;
	List p = l->next;
	l->next = p->next;
	x = p->x;
	y = p->y;
	ind = p->ind;
	free(p);
	return true;
}
//判断这个位置是终点2，还是墙0 还是可通行1
int Pass_or(int x,int y){ //判断这个位置是终点 2，还是墙0还是可通行1
	if(x==8&&y==1){
		return 2; 
	}else if(map[y][x]){
		return 1;
	}else{
		return 0;
	}
}
bool next(List &l, int x,int y,int ind){ //从x y往ind方向走
	map[y][x]=false;// 把当前位置设置成false 说明已经走过不能再走
	if(ind>3){ //所有方向都尝试过了 进入死胡同了，往回退一个
		if(!Pop(l,x,y,ind)) return false; //栈中空的 无路可退 ，则直接return false
		return next(l,x,y,ind); //回退位置往下个方向走
	}else{ //从x y往ind方向走
		List p;
		int next_x = x, next_y=y;
		if(ind == 0){ //往上走
			next_y -= 1;
		}else if(ind == 1){ //往左走 
			next_x -= 1;
		}else if(ind == 2){ //往下走
			next_y += 1;
		}else{ //往右走
			next_x += 1;
		}
		int flag = Pass_or(next_x, next_y); //判断下个位置是否可以走
		if(flag==1){ //下个方向可通行，则当前位置入栈，往下走
			Push(l,x,y,ind+1); //当前方向走过，那么ind+1
			return next(l,next_x,next_y,0);
		}else if(flag == 0){ //下个方向不能走
			return next(l,x,y,ind+1); //换个方向看看
		}else{ // 下个方向是终点 
			Push(l,x,y,ind+1); // 记录当前位置 
			return true; //返回true 
		}
	}
}
void print_map(){ //打印地图
	for(int i=0;i<10;i++){
		for(int j=0;j<10;j++){
			if(map[i][j]){
				printf(" ");
			}else{
				printf("#");
			}
		}
		printf("\n");
	}
}
int main(){
	List pass_in; //记录走过的路
	init(pass_in);
	printf("开始走迷宫"); //
	int x=1,y=1,ind=0; //从1开始
	if(next(pass_in,x,y,0)){ //迭代找路径 找到 返回true 没找到返回false
		printf("找到路径\n");
		print_L(pass_in);
	}else{
		printf("没找到路径\n");
	}
	return 0;
}

表达式求值

表达式求值是程序设计语言编译中的一个最基本问题。它的实现是栈应用的又一个典型例子。这里介绍一种简单直观、广为使用的算法，通常称为“算符优先法”

四则运算规则：
(1) 先乘除，后加减。
(2) 从左算到右。
(3) 先算括号内，后括号外。
算符优先法就是根据这个运算优先关系的规定来实现对表达式对编译或者执行的。
题目，输入一串表达式，通过栈实现它的正确运算
解题思路：用两个栈，一个栈用来存运算符+ - x / ()还有一个栈用来存运算数据。考虑到运算从左到右且有优先级，所以每次输入一个运算符，先判断是否优先级大于前面已存在的，如果是则入栈，如果小于前一个，则出栈前一个运算符和前一次的运算数据进行计算。
根据上述运算规则 运算 符优先级从低到高为( < -+ < *\ <)。考虑到int可用char类型存储，所以只定义一个栈结构体，数据域用char 数据栈用的时候类型强转下来减少代码量 好吧这样行不通，如果输入 10就会记录成两个数据，还是要两种不同的结构体来存放，而且深究下去如果输入的是小数还要增加很多判断。所以先写个简化的吧 。

#include<stdio.h>
#include<stdlib.h>
typedef struct CNode{
	char data; //存放运算符()+-x/ 
	struct CNode *next;
}CNode, *CList;

typedef struct NNode{
	float data; //存放数据
	struct NNode *next;
}NNode, *NList;
bool next(CList &cl,NList &nl, char e,bool &flag);
void print_N(NList &l){
	NList p = l->next;
	while(p!=NULL){
		printf("%f ",p->data);
		p = p->next;
	}
	printf("\n");
}
void init_c(CList &l){ //初始化一个头结点
	l = (CList)malloc(sizeof(CNode));
	l->next = NULL;
}
void init_n(NList &l){ //初始化一个头结点
	l = (NList)malloc(sizeof(NNode));
	l->next = NULL;
}
bool Pop_c(CList &l,char &e){
	if(l->next == NULL) return false;
	CList p = l->next;
	e = p->data;
	l->next = p->next;
	free(p);
	return true;
}
bool Pop_n(NList &l, float &e){
	if(l->next == NULL) return false;
	NList q = l->next;
	e = q->data;
	l->next = q->next;
	free(q);
	return true;
}
bool GetTop_c(CList &l,char &e){
	if(l->next == NULL) return false;
	e = l->next->data;
	return true;
}
bool GetTop_n(NList &l,float &e){
	if(l->next == NULL) return false;
	e = l->next->data;
	return true;
}
void Push_c(CList &l, char e){
	CList p = (CList)malloc(sizeof(CNode));
	p->data = e;
	p->next = l->next;
	l->next = p;
}
void Push_n(NList &l, float e){
	NList p = (NList)malloc(sizeof(NNode));	
	p->data = e;
	p->next = l->next;
	l->next = p;
}
float com_(float a,float b,char c){
	if(c=='+'){
		return a+b;
	}else if(c=='-'){
		return a-b;
	}else if(c=='*'){
		return a*b;
	}else{
		return a/b;
	}
}
bool cmp(CList cl,NList nl, char e){ //能进来说吗cl栈不空
	char le;
	float a,b,result; //运算符 和需要运算的两个数
	if(!Pop_c(cl,le)) return false;
	if(le=='('&&e==')') return true;//脱括弧
	if(!Pop_n(nl,a)||!Pop_n(nl,b)) return false; //出栈两个数字失败则返回false
	result = com_(b,a,le);
	Push_n(nl,result);
	if(e==')'){
		return cmp(cl,nl,e);
	}else{
		bool f = false;
		next(cl,nl,e,f);
	}
	return true;
}

bool next(CList &cl,NList &nl, char e,bool &flag){
	char le; //前一次
	if(e=='('){ //左括弧直接入栈
		flag = false;
		Push_c(cl,e);
	}else if(e=='+'||e=='-'){
		flag = false;
		if(!GetTop_c(cl,le)||le=='('){//为空栈 或 优先级低于它 
			Push_c(cl,e);
		}else{
			if(!cmp(cl,nl,e)) return false;//计算前面一步运算 false为计算失败
		}
	}else if(e=='*'||e=='/'){
		flag = false;
		if(!GetTop_c(cl,le)||le=='('||le=='+'||le=='-'){ //为空栈 或 优先级低于它
			Push_c(cl,e);
		}else{
			if(!cmp(cl,nl,e)) return false; //计算前面一步运算 false为计算失败
		}
	}else if(e==')'){//迭代脱括号 计算 false为计算失败
		flag = false;
		if(!cmp(cl,nl,e)) return false;
	}else{ //数据
		if(flag){ //为true说明上次输入也是数字
			float re;
			if(!Pop_n(nl,re)) return false;
			Push_n(nl,re*10+e-'0'); //把上次数字*10加上现在的。
		}else{
			Push_n(nl,e-'0');
		}
		flag = true;
	}
	return true;
}
void print_C(CList &l){
	CList p = l->next;
	while(p!=NULL){
		printf("%c ",p->data);
		p = p->next;
	}
	printf("\n");
}
int main(){
	CList cl;
	NList nl;
	init_c(cl);
	init_n(nl);
	char e;
	bool flag = false;
	scanf("%c",&e);
	while(e!='\n'){//输入回车结束
		if(!next(cl,nl,e,flag)){
			printf("计算错误。");
		}
		scanf("%c",&e);
	}
	while(cl->next!=NULL){
		float a=0.0,b=0.0,result; //运算符 和需要运算的两个数
		if(!Pop_c(cl,e)||!Pop_n(nl,a)||!Pop_n(nl,b)){
			printf("计算错误。");
			break;
		}
		result = com_(b,a,e);
		Push_n(nl,result);
	}
	if(nl->next!=NULL)
		printf("%f",nl->next->data);
	return 0;
}

这个题其实逻辑不复杂，对栈应用也很简单。主要是要考虑很多特殊情况所以写出来就比较复杂

栈与递归

栈还有一个重要应用是在程序设计语言中实现递归。一个直接调用自己或通过一系列的调用语句间接地调用自己的函数，称做递归函数。
递归是程序设计中一个强有力的工具。其一，有很多数学西数是递归定义的，如阶乘函数等;其二，有的数据结构，如二叉树、广义表等,由于结构本身固有的递归特性，则它们的操作可递归地描述;其三,还有一类问题，虽然问题本身没有明显的递归结构,但用递归求解比迭代求解更简单，如八皇后问题、Hanoi塔问题等。
这里就通过一个栈来实现Hanoi塔问题。
懒得打字，直接截图书上对Hanoi塔的介绍

代码如下，核心代码很简单，写的比较复杂，主要是为了可视化hanoi塔移动过程 (//核心算法就move和hanoi两个函数)

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
typedef struct Node{
	int data; //塔饼序号
	struct Node *next;// 下一个塔饼
}Node, *List;
void print_L(List &l){ 
	List p=l->next;
	while(p!=NULL){
		printf(" %d",p->data);
		p=p->next;
	}
	if(l->data==1)
		printf(" |x\n");
	else if(l->data==2)
		printf(" |y\n");
	else
		printf(" |z\n");
}
void print_hanoi(List &x, List &y, List &z){ //按x y z顺序打印表
	if(x->data<y->data){
		if(x->data<z->data){
			print_L(x);
			if(y->data<z->data){
				print_L(y);
				print_L(z);
			}else{
				print_L(z);
				print_L(y);
			}
		}else{
			print_L(z);
			print_L(x);
			print_L(y);
		}
	}else{
		if(y->data<z->data){
			print_L(y);
			if(x->data<z->data){
				print_L(x);
				print_L(z);
			}else{
				print_L(z);
				print_L(x);
			}
		}else{
			print_L(z);
			print_L(y);
			print_L(x);
		}
	}
	printf("\n");
}
void init(List &l){
	l = (List)malloc(sizeof(Node));
	l->data =0;// 头结点存放塔的顺序 x:1 y:2 z:3 方便后面打印时认塔
	l->next = NULL;
}
bool Pop(List &l,int &e){
	if(l->next == NULL) return false;
	List p = l->next;
	e = p->data;
	l->next=p->next;
	free(p);
	return true;
}
void Push(List &l,int &e){
	List p = (List)malloc(sizeof(Node));
	p->data = e;
	p->next = l->next;
	l->next = p;
}
//核心算法就move和hanoi两个 函数
bool move(List &l,List &r,int i){ //将序号为i的塔饼从l塔移动到r塔
	int e;
	if(!Pop(l,e)) return false; //出栈l栈顶元素
	if(e!=i) return false; //看看出栈元素是否是i 不是则出错
	Push(r,e); // 如果是将e入栈r
	return true;
}
bool hanoi(List &x, List &y, List &z,int n){  //将n个塔饼从x塔移动到z塔，利用y塔辅助 参数顺序，初始塔，辅助塔，目标塔， 移动数量
	if(n==1){
		move(x,z,1); //如果就一个直接移动
		print_hanoi(x,y,z);// 移动后打印下三个塔情况
		return true;
	}else{
		// 要将1 到 n个塔饼从x移动到z 则要先 将1 到 n-1个塔饼从x移动到y
		if(!hanoi(x,z,y,n-1)) return false;
		//然后将第n个塔饼直接从 x 移动到 z
		if(!move(x,z,n)) return false;
		print_hanoi(x,y,z);// 移动后打印下三个塔情况
		//然后将 y 上的1到n-1个塔饼移动到z上
		if(!hanoi(y,x,z,n-1)) return false;
	}
	return true;
}
void init_hanoi(List &x,List &y,List &z,int n){
	//初始化三个塔
	init(x);
	x->data = 1;
	init(y);
	y->data = 2;
	init(z);
	z->data = 3;
	while(n>0){ //从n到1入栈x
		Push(x,n);
		n--;
	}
}
int main(){
	//需要三个塔 x y z、
	List x,y,z;
	int n=10;//塔饼数量
	init_hanoi(x,y,z,n);
	print_hanoi(x,y,z);
	if(!hanoi(x,y,z,n)) //开始游戏返回 false说明出错
		printf("游戏失败");
	else
		printf("游戏成功");
	return 0;
}

队列

队列就跟我们生活中的排队一样的，先进先出，可以想像成一个管道，一边进一边出，所以先进去的先出来，而栈是一个只有一个口的井。 先进去的到里面了，后进的靠近井口所以先出来。
其实实现也是用线性表，只是有两个指针，一个头指针一个尾指针，进去时从尾部进 ，出来时从头部出。所以最好实现的就是链表。因为采用顺序表，多次出入队后，数组前面空间会有很多浪费。当然也可以采用循环线性表的思想实现来保证空间利用率。

队列的链表实现

#include<stdio.h>
#include<stdlib.h>
typedef int ElemType;
typedef struct QNode{ //链表中的结点类型
	ElemType data;
	struct QNode *next;
}QNode, *QueueP;
struct LinkQueue{ //链表包含指向一个链表头 尾的两个结点这 两个 指针指向的一连串结点构成一个链表
	QueueP front;
	QueueP rear;
};
void init_Queue(LinkQueue &queue){//初始化创建一个队列链表
	queue.front = queue.rear = (QueueP)malloc(sizeof(QNode));//头结点
	queue.front->next = NULL;//初始头结点next指向空
}
void EnQueue(LinkQueue &queue, ElemType e){ //入队
	QueueP q = (QueueP)malloc(sizeof(QNode)); // 创建一个结点q
	q->data = e; //数据存入结点
	q->next = NULL; //从尾部入队 所以next =NULL
	queue.rear->next = q; //原来尾部结点的next指向结点q
	queue.rear = q; //队列 的尾指针指向q
}
bool DeQueue(LinkQueue &queue, ElemType &e){//出队
	if(queue.front==queue.rear) return false;// 如果队列为空 返回false
	QueueP q = queue.front->next; //指向队列
	e = q->data;
	queue.front->next = q->next;
	if(q==queue.rear) queue.rear = queue.front; //出队的是最后一个结点，则rear=front队列空了
	free(q);
	return true;
}
void print_Q(LinkQueue &queue){
	QueueP p = queue.front->next; //从队列头开始
	while(p!=queue.rear){
		printf("%d",p->data);
		p = p->next;
	}
	printf("%d\n",p->data);
}
int main(){
	LinkQueue queue;
	int n;
	init_Queue(queue);
	EnQueue(queue,1);
	EnQueue(queue,2);
	EnQueue(queue,3);
	print_Q(queue);
	DeQueue(queue,n);
	printf("%d\n",n);
	print_Q(queue);
	return 0;
}

队列的循环线性表实现

首先因为用顺序线性表来实现，所以是一个在内存上连续的空间，然后用front rear分别指向逻辑上的队头和队尾。物理上就是数组的下标。考虑到队列先进先出，每次从队尾插入数据 从队头放入数据，所以当rear指向数组的最后一个单元时，head可能不在0号单元，从而出现了队尾没有 空间可以插入数据 ，但队头前面还有空间可以插入数据。
为了解决这个问题，提高空间利用率。从逻辑上可以 把数组的尾部和头部对接起来，形成一个回环，这样当数组头部有空间时，rear可以循环到头部放入数据，但这时候如何判断整个队伍放满了了。那就是当 rear再往后移动一位就和head重叠时。这时候整个队列 就只有rear所在下标的空间还没放元素。但我们就空出这个空间来方便队列的判空（因为这个空间也放入数据后，front就等于rear了，而这个是用来判断队列是否为空的）。
逻辑就这些，具体代码实现如下。

#include<stdio.h>
#include<stdlib.h>
#define MaxSize 100 //队列的最大长度
typedef int ElemType;
typedef struct { //链表中的结点类型
	ElemType *base; //指向一串连续的空间
	ElemType front; //队头所在位置
	ElemType rear;  //队尾所在位置
}SqList;

void init(SqList &l){
	//创建存放队的连续空间
	l.base = (ElemType *)malloc(MaxSize*sizeof(ElemType));
	l.front = l.rear = 0;
}
bool EnQueue(SqList &l, ElemType e){ // 入队
	if((l.rear+1)%MaxSize == l.front)  return false; //队列满了
	l.base[l.rear] = e;
	l.rear = (l.rear + 1) % MaxSize;
	return true;
}
bool DeQueue(SqList &l, ElemType &e){ // 出队
	if(l.rear==l.front) return false; //  队空的
	e = l.base[l.front];
	l.front = (l.front + 1) % MaxSize;
	return true;

}
void create(SqList &l, int n){//输入n个数创建一个队列 
	int scanf_n;
	while(n--){
		scanf("%d",&scanf_n);
		EnQueue(l,scanf_n);
	}
}
void print_Queue(SqList &l){ //打印队列中元素
	int i  = l.front;
	while(i!=l.rear){
		printf("%d ",l.base[i]);
		i = (i+1)% MaxSize;
	}
	printf("\n");
}
int main(){
	SqList l;
	int n;
	init(l);
	create(l,5);
	print_Queue(l);
	DeQueue(l,n);
	print_Queue(l);
	return 0;
}